Es un circuito donde un número cualquiera de elementos simples se conectan al mismo par de nodos.
Ejemplo:

La única tensión desconocida en este circuito es V1. Hay tres conexiones en este nodo y por esta razón, 3 corrientes a considerar. Ahora se analiza todas las corrientes que pasan por el nodo, así:

Con ley de corrientes de Kirchhoff (LCK), tenemos:

Se resuelve con respecto a V1:

Finalmente, la tensión desconocida se resuelve sustituyendo valores numéricos para cada variable. Después de haber obtenido estas ecuaciones y conocer cada tensión, es fácil calcular cualquier corriente desconocida.
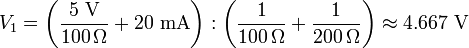
Supernodos
Esta combinación de los dos nodos es llamada el método de supernodo, y requiere una ecuación adicional, que involucre las tensiones que afectan a la fuente, V1 = V2 + VA.
El sistema de ecuaciones para este circuito es:

Al sustituir V1 en la primera ecuación y resolviendo con respecto a V2, tenemos: 

Ejemplo:
- Tensión en la resistencia de 4Ω:
- factorizando
- Observamos el supernodo en los nodos
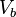 y
y  , tomamos estos dos nodos como uno solo, por lo tanto sumamos las corrientes de las resistencias que hay conectadas a
, tomamos estos dos nodos como uno solo, por lo tanto sumamos las corrientes de las resistencias que hay conectadas a
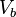 y
y  :
:
- factorizando
- Finalmente, planteamos una ecuación para la fuente de voltaje la cual es la caída de voltaje en los nodos así:
Observación:Debemos tener en cuenta la polaridad de la fuente para plantear esta última ecuación, y así obtener el sistema de ecuaciones para determinar los valores de los voltajes.
Sistema de ecuaciones: 

Resolviendo Va= 62,5 V, Vb= 22,5 V y Vc= 12,5 V
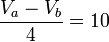



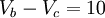
No hay comentarios.:
Publicar un comentario